复习一波最小割...
理论知识:

。
BZOJ1934 善意的投票
题意:n个人分别喜欢睡/不睡午觉。改变一个人的喜好要花费1代价。有m对朋友,每对朋友的喜好不同会产生1代价。求最小代价。
解:经典题了.....
每个人向s,t连边,求最小割。如果割掉某个边就代表选哪边。朋友之间连双向边,代表如果选的不同的话还要割一刀。
考虑为什么不会有点两条边都被割。因为两条边都被割表明有个跟它相连的没割上面,又有个跟它相连的没割下面,而这显然是不可能的,因为它们会通过这个点间接的出现一条流。


1 #include2 3 const int N = 3010, INF = 0x3f3f3f3f; 4 5 struct Edge { 6 int nex, v, c; 7 Edge(int NEX = 0, int V = 0, int C = 0) { 8 nex = NEX; 9 v = V;10 c = C;11 }12 }edge[2000010]; int tp = 1;13 14 int e[N], d[N], vis[N], Time, cur[N], cnt;15 std::queue Q;16 int n, a[N];17 18 inline void add(int x, int y, int z) {19 edge[++tp] = Edge(e[x], y, z);20 e[x] = tp;21 edge[++tp] = Edge(e[y], x, 0);22 e[y] = tp;23 return;24 }25 26 inline bool BFS(int s, int t) {27 Time++;28 vis[s] = Time;29 d[s] = 0;30 Q.push(s);31 while(Q.size()) {32 int x = Q.front();33 Q.pop();34 for(int i = e[x]; i; i = edge[i].nex) {35 int y = edge[i].v;36 if(vis[y] == Time || !edge[i].c) continue;37 vis[y] = Time;38 d[y] = d[x] + 1;39 Q.push(y);40 }41 }42 return vis[t] == Time;43 }44 45 int DFS(int x, int t, int maxF) {46 if(x == t) return maxF;47 int ans = 0;48 for(int i = cur[x]; i; i = edge[i].nex) {49 int y = edge[i].v;50 if(d[y] != d[x] + 1 || !edge[i].c) continue;51 int temp = DFS(y, t, std::min(edge[i].c, maxF - ans));52 if(!temp) d[y] = INF;53 ans += temp;54 edge[i].c -= temp;55 edge[i ^ 1].c += temp;56 if(ans == maxF) break;57 cur[x] = i;58 }59 return ans;60 }61 62 inline int solve(int s, int t) {63 int ans = 0;64 while(BFS(s, t)) {65 memcpy(cur + 1, e + 1, cnt * sizeof(int));66 ans += DFS(s, t, INF);67 }68 return ans;69 }70 71 int main() {72 int m;73 scanf("%d%d", &n, &m);74 int s = n + 1, t = n + 2;75 cnt = t;76 for(int i = 1; i <= n; i++) {77 scanf("%d", &a[i]);78 if(a[i]) {79 add(s, i, 1);80 }81 else {82 add(i, t, 1);83 }84 }85 for(int i = 1, x, y; i <= m; i++) {86 scanf("%d%d", &x, &y);87 add(x, y, 1);88 add(y, x, 1);89 }90 int ans = solve(s, t);91 printf("%d\n", ans);92 return 0;93 }
BZOJ2127 happiness
题意:n个人,m对朋友。每个人选文科,理科都分别有贡献,每对朋友同时选文/选理也有贡献。求最大贡献。
解:先设每个人同时选了文理。考虑割掉。
s向人连选文的贡献,人向t连选理的。一对朋友之间,考虑到如果有任一个选了文,就拿不到全选理的贡献,所以建图大概长这样...
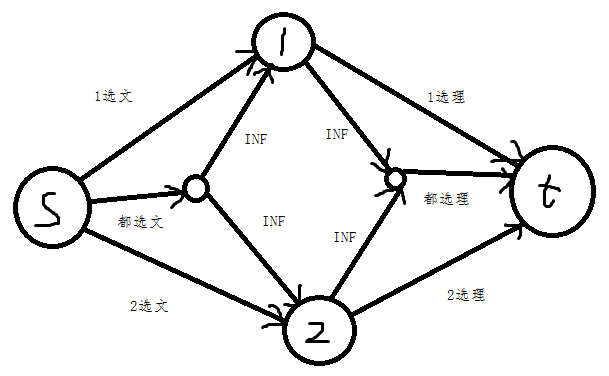
然后求最小割,拿总贡献减去,就是最大贡献了。


1 #include2 3 const int N = 100010, INF = 0x3f3f3f3f; 4 5 struct Edge { 6 int nex, v, c; 7 Edge(int NEX = 0, int V = 0, int C = 0) { 8 nex = NEX; 9 v = V; 10 c = C; 11 } 12 }edge[2000010]; int tp = 1; 13 14 int e[N], d[N], vis[N], Time, cur[N], cnt; 15 std::queue Q; 16 int n, m, s, t; 17 18 inline void add(int x, int y, int z) { 19 edge[++tp] = Edge(e[x], y, z); 20 e[x] = tp; 21 edge[++tp] = Edge(e[y], x, 0); 22 e[y] = tp; 23 return; 24 } 25 26 inline bool BFS(int s, int t) { 27 Time++; 28 vis[s] = Time; 29 d[s] = 0; 30 Q.push(s); 31 while(Q.size()) { 32 int x = Q.front(); 33 Q.pop(); 34 for(int i = e[x]; i; i = edge[i].nex) { 35 int y = edge[i].v; 36 if(vis[y] == Time || !edge[i].c) continue; 37 vis[y] = Time; 38 d[y] = d[x] + 1; 39 Q.push(y); 40 } 41 } 42 return vis[t] == Time; 43 } 44 45 int DFS(int x, int t, int maxF) { 46 if(x == t) return maxF; 47 int ans = 0; 48 for(int i = cur[x]; i; i = edge[i].nex) { 49 int y = edge[i].v; 50 if(d[y] != d[x] + 1 || !edge[i].c) continue; 51 int temp = DFS(y, t, std::min(edge[i].c, maxF - ans)); 52 if(!temp) d[y] = INF; 53 ans += temp; 54 edge[i].c -= temp; 55 edge[i ^ 1].c += temp; 56 if(ans == maxF) break; 57 cur[x] = i; 58 } 59 return ans; 60 } 61 62 inline int solve(int s, int t) { 63 int ans = 0; 64 while(BFS(s, t)) { 65 memcpy(cur + 1, e + 1, cnt * sizeof(int)); 66 ans += DFS(s, t, INF); 67 } 68 return ans; 69 } 70 71 inline int id(int i, int j) { 72 return (i - 1) * m + j; 73 } 74 75 int main() { 76 scanf("%d%d", &n, &m); 77 s = n * m + 1, t = s + 1; 78 int ans = 0, x; 79 cnt = t; 80 for(int i = 1; i <= n; i++) { 81 for(int j = 1; j <= m; j++) { 82 scanf("%d", &x); 83 ans += x; 84 add(s, id(i, j), x); 85 } 86 } 87 for(int i = 1; i <= n; i++) { 88 for(int j = 1; j <= m; j++) { 89 scanf("%d", &x); 90 ans += x; 91 add(id(i, j), t, x); 92 } 93 } 94 for(int i = 1; i < n; i++) { 95 for(int j = 1; j <= m; j++) { 96 scanf("%d", &x); 97 ans += x; 98 add(s, ++cnt, x); 99 add(cnt, id(i, j), INF);100 add(cnt, id(i + 1, j), INF);101 }102 }103 for(int i = 1; i < n; i++) {104 for(int j = 1; j <= m; j++) {105 scanf("%d", &x);106 ans += x;107 add(++cnt, t, x);108 add(id(i, j), cnt, INF);109 add(id(i + 1, j), cnt, INF);110 }111 }112 for(int i = 1; i <= n; i++) {113 for(int j = 1; j < m; j++) {114 scanf("%d", &x);115 ans += x;116 add(s, ++cnt, x);117 add(cnt, id(i, j), INF);118 add(cnt, id(i, j + 1), INF);119 }120 }121 for(int i = 1; i <= n; i++) {122 for(int j = 1; j < m; j++) {123 scanf("%d", &x);124 ans += x;125 add(++cnt, t, x);126 add(id(i, j), cnt, INF);127 add(id(i, j + 1), cnt, INF);128 }129 }130 ans -= solve(s, t);131 printf("%d\n", ans);132 return 0;133 }
注意这题建图画风跟别的题不一样,是因为按照之前的建图,当一对朋友同时选0的时候,仍要损失同时选1的代价,而这部分是我们难以计算的。
BZOJ1976 能量魔方
题意:有n3个块构成了立方体,有些位置填了0/1,别的地方自己填。6连通的块之间如果颜色不同就会有1贡献,求最大贡献。
解:前两题都是最大化相同,最小化不同,这题反其道而行之,何如?
考虑到这些格子和6连通关系构成了二分图。我们把其中一个部分全部反色,不就成了最大化相同吗?直接套用第一题的做法。


1 #include2 3 const int N = 100010, INF = 0x3f3f3f3f; 4 5 struct Edge { 6 int nex, v, c; 7 Edge(int NEX = 0, int V = 0, int C = 0) { 8 nex = NEX; 9 v = V; 10 c = C; 11 } 12 }edge[2000010]; int tp = 1; 13 14 int e[N], d[N], vis[N], Time, cur[N], cnt; 15 std::queue Q; 16 int n; 17 18 inline void add(int x, int y, int z) { 19 edge[++tp] = Edge(e[x], y, z); 20 e[x] = tp; 21 edge[++tp] = Edge(e[y], x, 0); 22 e[y] = tp; 23 return; 24 } 25 26 inline bool BFS(int s, int t) { 27 Time++; 28 vis[s] = Time; 29 d[s] = 0; 30 Q.push(s); 31 while(Q.size()) { 32 int x = Q.front(); 33 Q.pop(); 34 for(int i = e[x]; i; i = edge[i].nex) { 35 int y = edge[i].v; 36 if(vis[y] == Time || !edge[i].c) continue; 37 vis[y] = Time; 38 d[y] = d[x] + 1; 39 Q.push(y); 40 } 41 } 42 return vis[t] == Time; 43 } 44 45 int DFS(int x, int t, int maxF) { 46 if(x == t) return maxF; 47 int ans = 0; 48 for(int i = cur[x]; i; i = edge[i].nex) { 49 int y = edge[i].v; 50 if(d[y] != d[x] + 1 || !edge[i].c) continue; 51 int temp = DFS(y, t, std::min(edge[i].c, maxF - ans)); 52 if(!temp) d[y] = INF; 53 ans += temp; 54 edge[i].c -= temp; 55 edge[i ^ 1].c += temp; 56 if(ans == maxF) break; 57 cur[x] = i; 58 } 59 return ans; 60 } 61 62 inline int solve(int s, int t) { 63 int ans = 0; 64 while(BFS(s, t)) { 65 memcpy(cur + 1, e + 1, cnt * sizeof(int)); 66 ans += DFS(s, t, INF); 67 } 68 return ans; 69 } 70 71 inline int id(int x, int y, int z) { 72 return (x - 1) * n * n + (y - 1) * n + z; 73 } 74 75 char str[N]; 76 77 int main() { 78 scanf("%d", &n); 79 int s = n * n * n + 1, t = s + 1, ans = 0; 80 cnt = t; 81 for(int i = 1; i <= n; i++) { 82 for(int j = 1; j <= n; j++) { 83 scanf("%s", str + 1); 84 for(int k = 1; k <= n; k++) { 85 if(str[k] == '?'); 86 else if((str[k] == 'P') == ((i + j + k) & 1)) { 87 add(s, id(i, j, k), INF); 88 } 89 else { 90 add(id(i, j, k), t, INF); 91 } 92 93 if(i > 1) { 94 add(id(i, j, k), id(i - 1, j, k), 1); 95 add(id(i - 1, j, k), id(i, j, k), 1); 96 ans++; 97 } 98 if(j > 1) { 99 add(id(i, j, k), id(i, j - 1, k), 1);100 add(id(i, j - 1, k), id(i, j, k), 1);101 ans++;102 }103 if(k > 1) {104 add(id(i, j, k), id(i, j, k - 1), 1);105 add(id(i, j, k - 1), id(i, j, k), 1);106 ans++;107 }108 }109 }110 }111 printf("%d\n", ans - solve(s, t));112 return 0;113 }
BZOJ2132 圈地计划
题意:给你一个矩阵,每个位置放0有贡献,放1有贡献,4连通的格子放不同的还有贡献,求最大贡献。
解:类似上一题,黑白染色之后把黑色格子放的全部反转,就有相同相邻的格子会产生贡献。注意01分别的贡献也要相应的反转。
然后使用上一题的做法即可。


1 #include2 3 const int N = 100010, INF = 0x3f3f3f3f; 4 5 struct Edge { 6 int nex, v, c; 7 Edge(int NEX = 0, int V = 0, int C = 0) { 8 nex = NEX; 9 v = V; 10 c = C; 11 } 12 }edge[2000010]; int tp = 1; 13 14 int e[N], d[N], vis[N], Time, cur[N], cnt; 15 std::queue Q; 16 int n, m, a[101][101], b[101][101], c[101][101]; 17 18 inline void add(int x, int y, int z) { 19 edge[++tp] = Edge(e[x], y, z); 20 e[x] = tp; 21 edge[++tp] = Edge(e[y], x, 0); 22 e[y] = tp; 23 return; 24 } 25 26 inline bool BFS(int s, int t) { 27 Time++; 28 vis[s] = Time; 29 d[s] = 0; 30 Q.push(s); 31 while(Q.size()) { 32 int x = Q.front(); 33 Q.pop(); 34 for(int i = e[x]; i; i = edge[i].nex) { 35 int y = edge[i].v; 36 if(vis[y] == Time || !edge[i].c) continue; 37 vis[y] = Time; 38 d[y] = d[x] + 1; 39 Q.push(y); 40 } 41 } 42 return vis[t] == Time; 43 } 44 45 int DFS(int x, int t, int maxF) { 46 if(x == t) return maxF; 47 int ans = 0; 48 for(int i = cur[x]; i; i = edge[i].nex) { 49 int y = edge[i].v; 50 if(d[y] != d[x] + 1 || !edge[i].c) continue; 51 int temp = DFS(y, t, std::min(edge[i].c, maxF - ans)); 52 if(!temp) d[y] = INF; 53 ans += temp; 54 edge[i].c -= temp; 55 edge[i ^ 1].c += temp; 56 if(ans == maxF) break; 57 cur[x] = i; 58 } 59 return ans; 60 } 61 62 inline int solve(int s, int t) { 63 int ans = 0; 64 while(BFS(s, t)) { 65 memcpy(cur + 1, e + 1, cnt * sizeof(int)); 66 ans += DFS(s, t, INF); 67 } 68 return ans; 69 } 70 71 inline int id(int i, int j) { 72 return (i - 1) * m + j; 73 } 74 75 int main() { 76 scanf("%d%d", &n, &m); 77 int s = n * m + 1, t = s + 1, ans = 0; 78 cnt = t; 79 for(int i = 1; i <= n; i++) { 80 for(int j = 1; j <= m; j++) { 81 scanf("%d", &a[i][j]); 82 ans += a[i][j]; 83 } 84 } 85 for(int i = 1; i <= n; i++) { 86 for(int j = 1; j <= m; j++) { 87 scanf("%d", &b[i][j]); 88 ans += b[i][j]; 89 if((i + j) & 1) { 90 std::swap(a[i][j], b[i][j]); 91 } 92 add(s, id(i, j), a[i][j]); 93 add(id(i, j), t, b[i][j]); 94 } 95 } 96 for(int i = 1; i <= n; i++) { 97 for(int j = 1; j <= m; j++) { 98 scanf("%d", &c[i][j]); 99 if(i > 1) {100 add(id(i, j), id(i - 1, j), c[i][j] + c[i - 1][j]);101 add(id(i - 1, j), id(i, j), c[i][j] + c[i - 1][j]);102 ans += c[i][j] + c[i - 1][j];103 }104 if(j > 1) {105 add(id(i, j), id(i, j - 1), c[i][j] + c[i][j - 1]);106 add(id(i, j - 1), id(i, j), c[i][j] + c[i][j - 1]);107 ans += c[i][j] + c[i][j - 1];108 }109 }110 }111 112 printf("%d\n", ans - solve(s, t));113 114 return 0;115 }
LOJ#2146 寿司餐厅
题意:有个寿司序列,每个子串都有个价值,每个寿司有个种类。你可以无限次的取,每次取一个子串,那么就能得到这个子串的所有子串的贡献。但是每个子串[l, r]的贡献不管取了多少次都只会算一次。如果最终这n个寿司中你吃到过其中i(i > 0)个x种类的寿司,那么就要付出m * x * x + i * x的钱。求你能得到的最大(总价值 - 钱数)。
解:在那想50分状压怎么做,结果想着就把正解搞出来了,状压还是不会...
画出矩形来,发现每次就是取一个左下角的前缀和,相当于取了一个点就要取它左下的所有点。这是最大权闭合子图。然后怎么算付的钱呢?每个寿司(就是i,i那个位置)连到一个(-x)的点。然后所有(-x)的点再连到一个(-x2)的点即可。


1 #include2 3 const int N = 110, M = 100010, INF = 0x3f3f3f3f; 4 5 struct Edge { 6 int nex, v, c; 7 Edge(int NEX = 0, int V = 0, int C = 0) { 8 nex = NEX; 9 v = V; 10 c = C; 11 } 12 }edge[2000010]; int tp = 1; 13 14 int e[M], a[N], d[N][N], n, m, val[M], dis[M], vis[M], Time, cnt, cur[M], id[N][N], use[1010]; 15 std::queue Q; 16 17 inline void add(int x, int y, int z) { 18 //printf("add %d %d %d \n", x, y, z); 19 edge[++tp] = Edge(e[x], y, z); 20 e[x] = tp; 21 edge[++tp] = Edge(e[y], x, 0); 22 e[y] = tp; 23 return; 24 } 25 26 inline bool BFS(int s, int t) { 27 Time++; 28 vis[s] = Time; 29 dis[s] = 0; 30 Q.push(s); 31 while(Q.size()) { 32 int x = Q.front(); 33 Q.pop(); 34 //printf("BFS x = %d \n", x); 35 for(int i = e[x]; i; i = edge[i].nex) { 36 int y = edge[i].v; 37 if(vis[y] == Time || !edge[i].c) { 38 continue; 39 } 40 //printf("BFS %d -> %d \n", x, y); 41 vis[y] = Time; 42 dis[y] = dis[x] + 1; 43 Q.push(y); 44 } 45 } 46 return vis[t] == Time; 47 } 48 49 int DFS(int x, int t, int maxF) { 50 if(x == t) { 51 //printf("x == t maxF = %d \n", maxF); 52 return maxF; 53 } 54 int ans = 0; 55 for(int i = cur[x]; i; i = edge[i].nex) { 56 int y = edge[i].v; 57 if(dis[y] != dis[x] + 1 || !edge[i].c) continue; 58 int temp = DFS(y, t, std::min(maxF - ans, edge[i].c)); 59 //printf("DFS %d -> %d min %d %d \n", x, y, maxF - ans, edge[i].c); 60 if(!temp) dis[y] = INF; 61 ans += temp; 62 edge[i].c -= temp; 63 edge[i ^ 1].c += temp; 64 if(ans == maxF) break; 65 cur[x] = i; 66 } 67 return ans; 68 } 69 70 inline int solve(int s, int t) { 71 int ans = 0; 72 while(BFS(s, t)) { 73 memcpy(cur + 1, e + 1, cnt * sizeof(int)); 74 //int temp = DFS(s, t, INF); 75 //printf("ans += %d \n", temp); 76 ans += DFS(s, t, INF); 77 78 } 79 return ans; 80 } 81 82 inline bool valid(int x, int y) { 83 if(!x || !y || x > n || y > n) return false; 84 return y >= x; 85 } 86 87 int main() { 88 scanf("%d%d", &n, &m); 89 int s = 1, t = 2, ans = 0; 90 cnt = t; 91 for(int i = 1; i <= n; i++) { 92 scanf("%d", &a[i]); 93 } 94 for(int i = 1; i <= n; i++) { 95 for(int j = i; j <= n; j++) { 96 scanf("%d", &d[i][j]); 97 id[i][j] = ++cnt; 98 if(d[i][j] > 0) { 99 add(s, id[i][j], d[i][j]);100 ans += d[i][j];101 }102 else if(d[i][j] < 0) {103 add(id[i][j], t, -d[i][j]);104 }105 if(valid(i, j - 1)) {106 add(id[i][j], id[i][j - 1], INF);107 }108 if(valid(i - 1, j)) {109 add(id[i - 1][j], id[i][j], INF);110 }111 }112 add(id[i][i], ++cnt, INF);113 add(cnt, t, a[i]);114 if(m) {115 if(!use[a[i]]) {116 use[a[i]] = ++cnt;117 add(cnt - 1, cnt, INF);118 add(cnt, t, a[i] * a[i]);119 }120 else {121 add(cnt, use[a[i]], INF);122 }123 }124 }125 126 printf("%d", ans - solve(s, t));127 return 0;128 }
去膜了一下官方题解,发现这SB题没有状压做法......当m = 0的时候可以直接区间DP预处理每一段全选的最大价值,然后再在序列上按照断点DP。
如果能够重复计算一个子串的贡献呢?不会......
BZOJ3996 线性代数
题意:给出一个N * N的矩阵B和一个1 * N的矩阵C。求出一个1 * N的01矩阵A,使得D = (A * B - C) * AT最大。输出D。
解:暴力推一波式子,发现D = ∑(∑(AiAjBij) - AiCi),由于A是01矩阵,所以相当于选出若干个B,如果Bij被选,那么-Ci和-Cj也会被选。求最大价值。最大权闭合子图。


1 #include2 3 const int N = 260010, INF = 0x3f3f3f3f; 4 5 struct Edge { 6 int nex, v, c; 7 Edge(int NEX = 0, int V = 0, int C = 0) { 8 nex = NEX; 9 v = V; 10 c = C; 11 } 12 }edge[2000010]; int tp = 1; 13 14 int e[N], cur[N], d[N], vis[N], Time, cnt, n; 15 std::queue Q; 16 17 inline void add(int x, int y, int z) { 18 //printf("add %d %d \n", x, y); 19 edge[++tp] = Edge(e[x], y, z); 20 e[x] = tp; 21 edge[++tp] = Edge(e[y], x, 0); 22 e[y] = tp; 23 return; 24 } 25 26 inline bool BFS(int s, int t) { 27 Time++; 28 vis[s] = Time; 29 d[s] = 0; 30 Q.push(s); 31 while(Q.size()) { 32 int x = Q.front(); 33 Q.pop(); 34 for(int i = e[x]; i; i = edge[i].nex) { 35 int y = edge[i].v; 36 if(vis[y] == Time || !edge[i].c) { 37 continue; 38 } 39 vis[y] = Time; 40 d[y] = d[x] + 1; 41 Q.push(y); 42 } 43 } 44 return vis[t] == Time; 45 } 46 47 int DFS(int x, int t, int maxF) { 48 if(x == t) { 49 return maxF; 50 } 51 int ans = 0; 52 for(int i = cur[x]; i; i = edge[i].nex) { 53 int y = edge[i].v; 54 if(d[y] != d[x] + 1 || !edge[i].c) continue; 55 int temp = DFS(y, t, std::min(maxF - ans, edge[i].c)); 56 if(!temp) d[y] = INF; 57 ans += temp; 58 edge[i].c -= temp; 59 edge[i ^ 1].c += temp; 60 if(ans == maxF) break; 61 cur[x] = i; 62 } 63 return ans; 64 } 65 66 inline int solve(int s, int t) { 67 int ans = 0; 68 while(BFS(s, t)) { 69 memcpy(cur + 1, e + 1, cnt * sizeof(int)); 70 ans += DFS(s, t, INF); 71 } 72 return ans; 73 } 74 75 inline int id(int i, int j) { 76 return (i - 1) * n + j; 77 } 78 79 int main() { 80 scanf("%d", &n); 81 int s = n * (n + 1) + 1, t = s + 1, ans = 0, x; 82 cnt = t; 83 for(int i = 1; i <= n; i++) { 84 for(int j = 1; j <= n; j++) { 85 scanf("%d", &x); 86 if(x > 0) { 87 add(s, id(i, j), x); 88 ans += x; 89 } 90 else if(x < 0) { 91 add(id(i, j), t, -x); 92 } 93 add(id(i, j), id(n + 1, i), INF); 94 add(id(i, j), id(n + 1, j), INF); 95 } 96 } 97 for(int i = 1; i <= n; i++) { 98 scanf("%d", &x); 99 x = -x;100 if(x > 0) {101 add(s, id(n + 1, i), x);102 ans += x;103 }104 else if(x < 0) {105 add(id(n + 1, i), t, -x);106 }107 }108 109 printf("%d", ans - solve(s, t));110 return 0;111 }
BZOJ3218 a + b Problem
题意:给你个序列,你要黑白染色。分别有贡献。每个位置还有权值。如果某个黑色位置前面有白色位置,且那个白色位置的权值在一个特定的限制中,那么要减去一个代价。求最大贡献。
解:按照前面几题最小割的套路,我们要把每个点向它前面符合条件的白点连边。注意到这些白点是二维矩阵内的,于是主席树优化一下。


1 #include2 3 typedef long long LL; 4 const int N = 200010; 5 const LL INF = 0x3f3f3f3f3f3f3f3fll; 6 7 struct Edge { 8 int nex, v; 9 LL c; 10 Edge(int NEX = 0, int V = 0, LL C = 0) { 11 nex = NEX; 12 v = V; 13 c = C; 14 } 15 }edge[500010]; int tp = 1; 16 17 int e[N], cur[N], d[N], vis[N], Time, cnt; 18 std::queue Q; 19 int n, a[N], lc[N], rc[N], rt[N], last[N]; 20 LL b[N], w[N], c[N]; 21 int ls[N], rs[N], X[N], xx; 22 23 inline void add(int x, int y, LL z) { 24 //if(x == n * 2 + 1 || y == n * 2 + 2) { 25 //printf("%d %d %lld \n", x, y, z); 26 //} 27 edge[++tp] = Edge(e[x], y, z); 28 e[x] = tp; 29 edge[++tp] = Edge(e[y], x, 0); 30 e[y] = tp; 31 return; 32 } 33 34 inline bool BFS(int s, int t) { 35 Time++; 36 vis[s] = Time; 37 d[s] = 0; 38 Q.push(s); 39 while(Q.size()) { 40 int x = Q.front(); 41 Q.pop(); 42 for(int i = e[x]; i; i = edge[i].nex) { 43 int y = edge[i].v; 44 if(vis[y] == Time || !edge[i].c) { 45 continue; 46 } 47 vis[y] = Time; 48 d[y] = d[x] + 1; 49 Q.push(y); 50 } 51 } 52 return vis[t] == Time; 53 } 54 55 LL DFS(int x, int t, LL maxF) { 56 if(x == t) { 57 return maxF; 58 } 59 LL ans = 0; 60 for(int i = cur[x]; i; i = edge[i].nex) { 61 int y = edge[i].v; 62 if(d[y] != d[x] + 1 || !edge[i].c) continue; 63 LL temp = DFS(y, t, std::min(maxF - ans, edge[i].c)); 64 if(!temp) d[y] = INF; 65 ans += temp; 66 edge[i].c -= temp; 67 edge[i ^ 1].c += temp; 68 if(ans == maxF) break; 69 cur[x] = i; 70 } 71 return ans; 72 } 73 74 inline LL solve(int s, int t) { 75 LL ans = 0; 76 while(BFS(s, t)) { 77 memcpy(cur + 1, e + 1, cnt * sizeof(int)); 78 ans += DFS(s, t, INF); 79 } 80 return ans; 81 } 82 83 void insert(int &x, int y, int p, int v, int l, int r) { 84 if(!x || x == y) { 85 x = ++cnt; 86 ls[x] = ls[y]; 87 rs[x] = rs[y]; 88 } 89 //printf("insert x = %d \n", x); 90 if(l == r) { 91 if(last[r]) { 92 add(x, last[r], INF); 93 } 94 add(x, v, INF); 95 last[r] = x; 96 return; 97 } 98 int mid = (l + r) >> 1; 99 if(p <= mid) {100 insert(ls[x], ls[y], p, v, l, mid);101 }102 else {103 insert(rs[x], rs[y], p, v, mid + 1, r);104 }105 return;106 }107 108 void link(int L, int R, int v, int l, int r, int o) {109 if(!o) return;110 if(L <= l && r <= R) {111 add(v, o, INF);112 return;113 }114 int mid = (l + r) >> 1;115 if(L <= mid) link(L, R, v, l, mid, ls[o]);116 if(mid < R) link(L, R, v, mid + 1, r, rs[o]);117 return;118 }119 120 void build(int l, int r, int o) {121 if(!o || vis[o]) return;122 vis[o] = 1;123 int mid = (l + r) >> 1;124 if(ls[o]) {125 add(o, ls[o], INF);126 build(l, mid, ls[o]);127 }128 if(rs[o]) {129 add(o, rs[o], INF);130 build(mid + 1, r, rs[o]);131 }132 return;133 }134 135 int main() {136 137 //printf("%d \n", (sizeof(edge) + sizeof(e) * 12 + sizeof(b) * 3) / 1048576);138 139 scanf("%d", &n);140 int s = n * 2 + 1, t = s + 1;141 cnt = t;142 for(int i = 1; i <= n; i++) {143 scanf("%d%lld%lld%d%d%lld", &a[i], &b[i], &w[i], &lc[i], &rc[i], &c[i]);144 X[i] = a[i];145 }146 std::sort(X + 1, X + n + 1);147 xx = std::unique(X + 1, X + n + 1) - X - 1;148 for(int i = 1; i <= n; i++) {149 a[i] = std::lower_bound(X + 1, X + xx + 1, a[i]) - X;150 lc[i] = std::lower_bound(X + 1, X + xx + 1, lc[i]) - X;151 rc[i] = std::upper_bound(X + 1, X + xx + 1, rc[i]) - X - 1;152 if(i < n) {153 insert(rt[i], rt[i - 1], a[i], i, 1, xx);154 //printf("i = %d \n", i);155 }156 }157 158 LL ans = 0;159 160 for(int i = 1; i <= n; i++) {161 add(s, i, b[i]);162 add(i, t, w[i]);163 ans += b[i] + w[i];164 if(lc[i] > rc[i]) {165 continue;166 }167 if(i > 1) {168 add(i, i + n, c[i]);169 link(lc[i], rc[i], i + n, 1, xx, rt[i - 1]);170 }171 }172 ++Time;173 for(int i = 1; i < n; i++) build(1, xx, rt[i]);174 175 printf("%lld\n", ans - solve(s, t));176 return 0;177 }
BZOJ4501 旅行
题意:给定一张有向图,你要删去一些边,使得从1出发随机前进的期望长度最长。有些限制是删a边则必删b边,保证a和b起点相同。
解:发现这个起点相同很妙啊,那么这些点就是互相独立的了。然后逆拓扑序考虑。对每个点来说,我们要让∑(aivi) / ∑ai最大。
发现这是01分数规划问题,于是二分答案,就是求∑ai(vi - k)的最大值,且有些限制是不选a则一定不选b。于是先全部选了,就是选a一定选b,求最小权闭合子图即可。


1 #include2 3 typedef long long LL; 4 const int N = 20010; 5 const double INF = 1e9; 6 const double eps = 1e-12; 7 8 struct Edge { 9 int nex, v; 10 double c; 11 Edge(int NEX = 0, int V = 0, double C = 0) { 12 nex = NEX; 13 v = V; 14 c = C; 15 } 16 }edge[500010]; int tp = 1; 17 18 struct Node { 19 int l, r; 20 }node[N]; 21 22 int e[N], cur[N], d[N], vis[N], Time, cnt; 23 std::queue Q; 24 std::vector v[N], v2[N]; 25 double val[N], Val[N]; 26 int n, m, K, e2[N], in[N], topo[N], tp2, posu[N], posv[N], in2[N], id[N]; 27 Edge edge2[N]; 28 29 inline void add(int x, int y, double z) { 30 edge[++tp] = Edge(e[x], y, z); 31 e[x] = tp; 32 edge[++tp] = Edge(e[y], x, 0); 33 e[y] = tp; 34 return; 35 } 36 37 inline bool BFS(int s, int t) { 38 Time++; 39 vis[s] = Time; 40 d[s] = 0; 41 Q.push(s); 42 while(Q.size()) { 43 int x = Q.front(); 44 Q.pop(); 45 for(int i = e[x]; i; i = edge[i].nex) { 46 int y = edge[i].v; 47 if(vis[y] == Time || edge[i].c < eps) { 48 continue; 49 } 50 vis[y] = Time; 51 d[y] = d[x] + 1; 52 Q.push(y); 53 } 54 } 55 return vis[t] == Time; 56 } 57 58 double DFS(int x, int t, double maxF) { 59 if(x == t) { 60 return maxF; 61 } 62 double ans = 0; 63 for(int i = cur[x]; i; i = edge[i].nex) { 64 int y = edge[i].v; 65 if(d[y] != d[x] + 1 || edge[i].c < eps) continue; 66 double temp = DFS(y, t, std::min(maxF - ans, edge[i].c)); 67 if(temp < eps) d[y] = INF; 68 ans += temp; 69 edge[i].c -= temp; 70 edge[i ^ 1].c += temp; 71 if(fabs(ans - maxF) < eps) break; 72 cur[x] = i; 73 } 74 return ans; 75 } 76 77 inline double solve(int s, int t) { 78 double ans = 0; 79 while(BFS(s, t)) { 80 memcpy(cur + 1, e + 1, cnt * sizeof(int)); 81 ans += DFS(s, t, INF); 82 } 83 return ans; 84 } 85 86 /// --------------------------- Dinic ------------------------------------- 87 88 inline void add2(int x, int y) { 89 edge2[++tp2] = Edge(e2[x], y); 90 e2[x] = tp2; 91 return; 92 } 93 94 inline bool check(int x, double k) { 95 96 tp = 1; 97 memset(e + 1, 0, cnt * sizeof(int)); 98 99 int s = 1, t = 2;100 cnt = t;101 double ans = 0, tans = 0;102 for(int i = 0; i < v2[x].size(); i++) {103 int y = posv[v2[x][i]];104 Val[y] = val[y] - k;105 tans += Val[y];106 Val[y] = -Val[y];107 id[v2[x][i]] = ++cnt;108 if(Val[y] > eps) {109 add(s, cnt, Val[y]);110 ans += Val[y];111 }112 else if(Val[y] < -eps) {113 add(cnt, t, -Val[y]);114 }115 }116 117 for(int i = 0; i < v[x].size(); i++) {118 int t = v[x][i];119 add(id[node[t].l], id[node[t].r], INF);120 }121 122 ans -= solve(s, t);123 tans += ans;124 return tans > eps;125 }126 /*127 3 3 1128 1 2129 1 3130 2 3131 1 2132 133 */134 int main() {135 136 scanf("%d%d%d", &n, &m, &K);137 for(int i = 1, x, y; i <= m; i++) {138 scanf("%d%d", &x, &y);139 add2(x, y);140 v2[x].push_back(i);141 posu[i] = x;142 posv[i] = y;143 in[y]++;144 in2[x]++;145 }146 for(int i = 1, x, y; i <= K; i++) {147 scanf("%d%d", &node[i].r, &node[i].l);148 v[posu[node[i].l]].push_back(i);149 }150 151 for(int i = 1; i <= n; i++) {152 if(!in[i]) Q.push(i);153 }154 while(Q.size()) {155 int x = Q.front();156 Q.pop();157 topo[++cnt] = x;158 for(int i = e2[x]; i; i = edge2[i].nex) {159 int y = edge2[i].v;160 in[y]--;161 if(!in[y]) {162 Q.push(y);163 }164 }165 }166 167 cnt = 0;168 for(int alpha = n; alpha >= 1; alpha--) {169 int x = topo[alpha];170 if(!in2[x]) {171 continue;172 }173 if(!v[x].size()) {174 for(int i = e2[x]; i; i = edge2[i].nex) {175 int y = edge2[i].v;176 val[x] = std::max(val[x], val[y]);177 }178 val[x] = val[x] + 1;179 continue;180 }181 double l = 0, r = m;182 for(int beta = 1; beta <= 40; beta++) {183 double mid = (l + r) / 2;184 if(check(x, mid)) {185 l = mid;186 }187 else {188 r = mid;189 }190 }191 val[x] = r + 1;192 if(x == 1) break;193 }194 printf("%.6f\n", val[1]);195 return 0;196 }